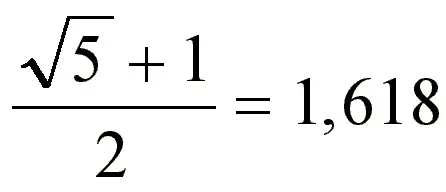Doğadaki Altın Oran: Fibonacci Dizisi

İnsanlık tarihinin en başından beri doğadaki etkileyici düzen, gözlem ve sorgulama yetenekleri gelişmiş insanlara ilham kaynağı olmuştur. Bu düzenin arkasındaki matematiksel temel olan Fibonacci Dizisi ve altın oranı açıklayan Leonardo Fibonacci; yıllardır bilim, sanat, mimarlık gibi pek çok alana ışık tutmuştur.

İtalyan matematikçi Leonardo Fibonacci, 13. yüzyılın başlarında önemli matematiksel çalışmalara imza atmıştır. Çocukluğunda babası Cezayir, Mısır ve Suriye’deki limanlarda çalıştığı için oralarda yaşayan ve oradaki Müslüman bilim insanlarından öğrendiklerini kitap haline getiren Fibonacci, matematiği Afrika'dan Avrupa'ya taşıyan bilim insanı olarak bilinir. Avrupa’da Romen rakamları kullanılırken ve sıfır kavramı bilinmezken Fibonacci; Arap rakamlarını, sıfırı ve ondalık sayı sistemini onlara öğretmiştir.  

1202 yılında yazdığı “Hesaplama Kitabı” anlamına gelen “Liber Abaci” eseri, Avrupa’nın bilimde ilerlemesinde önemli bir rol oynamıştır. Kitapta sayıların arasındaki ilişkiler ve matematik problemlerin ele alınmıştır. Kendi adını verdiği Fibonacci Dizisi’nden de burada bahseder.

Birçok bilimsel araştırmaya kaynak olan Fibonacci Dizisi günümüzde bilgisayar programlama, mimarlık, sanat tarihi gibi konuları anlatan hemen her ders kitabında yer alır. Fibonacci, Liber Abaci adlı kitabında bu diziyi açıklamak için tavşan problemini kullanırken, kolay anlaşılır olması için varsayımlarda bulunur. Bu varsayımlar şöyledir:

Tavşan çiftleri incelenirken bir tavşan erkek, bir tavşan dişi kabul edilir.
Her tavşan çiftinin 2 aydan sonra yavruları olabilir.
Aylar arasında fark gözetilmez ve yavruların her ayın ilk günü doğduğu kabul edilir.
Her çift yavrulamaya başladıkları aydan itibaren her ay biri erkek biri dişi olan bir çift yavru doğurur.
Bir yıl süreyle hiçbir tavşan ölmez.

Fibonacci varsayımları bu şekilde ele aldıktan sonra şu soruyu sorar:
“1 Ocak günü yeni doğmuş bir erkek ve bir dişi tavşandan oluşan bir tavşan çifti alsak, bir yıl sonra kaç çift tavşanımız olur?”

Bu soruyu yanıtlamak için varsayımlara göre her ay toplamda kaç tane tavşanın olduğunun çetelesini tutar:
1 Ocak’ta, yeni doğmuş 1 tavşanımız vardır.
1 Şubat’ta, tavşanlar yavrulayacak kadar büyümediği için hala 1 çift tavşanımız vardır.
1 Mart’ta, ilk çiftimizden ilk yavru çift doğar ve 2 çift tavşanımız olur.
1 Nisan’da, ilk çiftin tekrar iki yavrusu olur ancak mart ayında doğan yavruların henüz yavrusu olmaz. Toplam tavşan sayısı 3 çift olur.
1 Mayıs’ta, ocak ve martta doğan çiftlerden birer çift doğar, nisan doğumlu çiftler henüz yavru veremez. Toplam tavşan sayısı 5 çift olur.
1 Haziran’da; ocak, mart ve nisan doğumlu çiftler birer çift yavru verir, mayıs doğumlu çiftler henüz yavru vermez. Toplam tavşan sayımız 8 çift olur.
1 Temmuz’da; ocak, mart, nisan ve mayıs doğumlu çiftler birer çift yavru verir, haziran doğumlu çiftler henüz yavru vermez. Toplam tavşan sayımız 13 çift olur.
1 Ağustos'ta; ocak, mart, nisan, mayıs ve haziran doğumlu çiftler birer çift yavru verir, temmuz doğumlu çiftler henüz yavru vermez. Toplam tavşan sayımız 21 çift olur.
1 Eylül’de; ocak, mart, nisan, mayıs, haziran ve temmuz doğumlu çiftler birer çift yavru verir, ağustos doğumlu çiftler henüz yavru vermez. Toplam tavşan sayımız 34 çift olur.
1 Ekim’de; ocak, mart, nisan, mayıs, haziran, temmuz ve ağustos doğumlu çiftler birer çift yavru verir, eylül doğumlu çiftler henüz yavru vermez. Toplam tavşan sayımız 55 çift olur.
1 Kasım’da; ocak, mart, nisan, mayıs, haziran, temmuz, ağustos ve eylül doğumlu çiftler birer çift yavru verir, ekim doğumlu çiftler henüz yavru vermez. Toplam tavşan sayımız 89 çift olur.
1 Aralık’ta; ocak, mart, nisan, mayıs, haziran, temmuz, ağustos, eylül ve ekim doğumlu çiftler birer çift yavru verir, kasım doğumlu çiftler henüz yavru vermez. Toplam tavşan sayımız 144 çift olur.

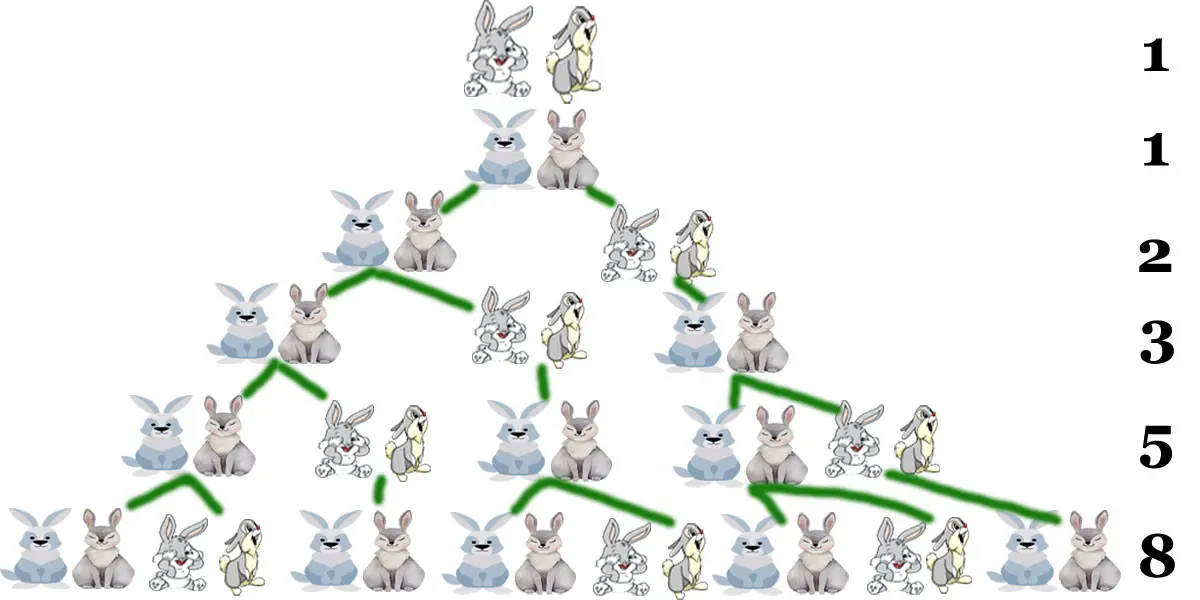
Fibonacci elde ettiği tavşan sayılarını bir dizi şeklinde yazar:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144

Ve bu diziyi özelleştiren şu özelliği fark eder: Dizideki bir sayı ile ondan bir önceki sayı toplandığında kendinden sonraki sayı elde edilmektedir.

Ayrıca bu diziyi detaylı inceleyen Fibonacci bir özelliğini daha görür. Fibonacci Sayı Dizisindeki ilk sayıdan sonraki her sayıyı kendinden önce gelen sayıya bölersek sonuç “altın oran” olarak ifade edilen 1,618 sayısına yaklaşılır.

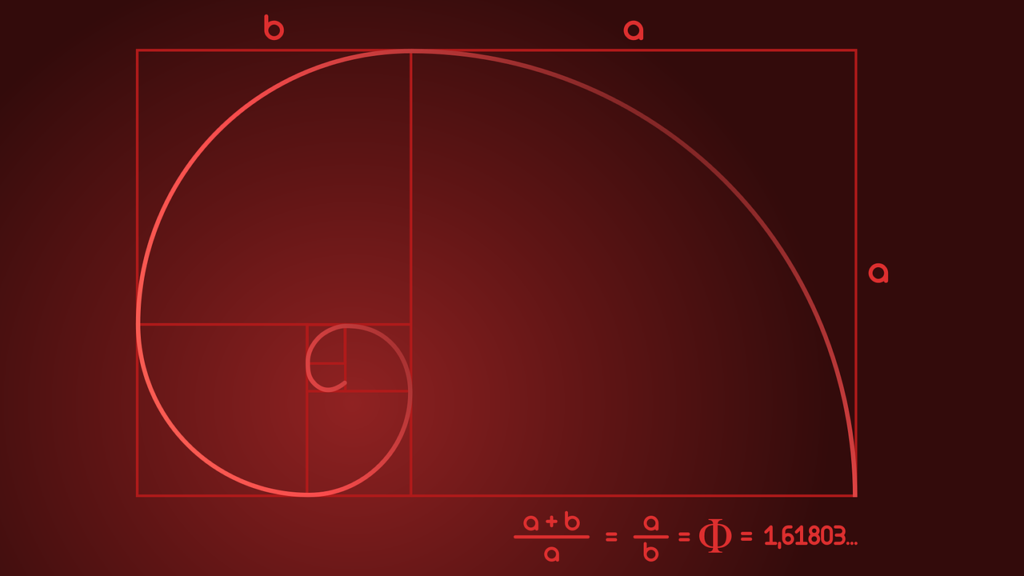
Altın oran (φ ≈ 1.618), bir nesnenin bir parçasının, diğer parçaya oranının, tüm nesnenin diğer parçasına oranıyla aynı olduğu bir matematiksel orandır. Fibonacci Dizisinde bir sayının kendisinden önce gelen sayıya bölünmesiyle elde edilen altın oran, Fibonacci Dikdörtgeninde de karşımıza çıkar. Bu dikdörtgene “Altın Dikdörtgen” de denir. Bu dikdörtgeni elde etmek için aynı büyüklükte iki kare yan yana getirilir, sonra bu iki kareye bitişik olacak şekilde büyük tek bir kare, ardından çizilen üç kareye bitişik bir kare daha eklenir. Bu şekilde bir araya getirilen kareler, kendilerinden önce komşu oldukları kare sayıları ile numaralandırıldığında Fibonacci Sayı Dizisine ulaşılır. Üstelik bu dikdörtgenin kenarlarının birbirine oranı da altın oranı vermektedir. Günümüze kullandığımız kredi kartları, bankamatikler ve A4 kağıtları Altın Dikdörtgendir.

Doğadaki detaylarda, tarihi eserlerle, ünlü tablolarda, meşhur mimari yapılarda altın orana rastlanır.

Doğayı incelediğimizde pek çok yerde altın oranı görebiliriz. Deniz kabukları, çiçek yaprakları, koni şeklindeki sarmallar ve bitki dalları gibi doğal yapılar, altın oranın izlerini taşır.
Bir ayçiçeğine veya bir çam kozalağına yakından bakıldığında merkezden dışa doğru sarmallar çizdiğini görülür. Salyangozların kabukları da altın orana sahip sarmal şeklindedir.

Herhangi bir sarmal biçimi içermeyen diğer canlılarda mesela ağaçlarda ve çiçek yapraklarında ise altın oran kendini farklı şekilde gösterir. Birçok ağacın dal ve yaprakları altın orana göre dizilmiştir.

İnsan anatomisi detaylı olarak incelendiğinde yüzümüzde, kemik yapımızda hatta iç organlarımızda da altın oran görülür. Örneğin sağlıklı bir insan vücudunda; ayak parmak uçlarından göbeğe olan uzunluğun göbekten baş bitimine olan uzunluğa oranı, dizden bileğe olan uzunluğun, dizden bele olan uzunluğa oranı, çeneden alın bitimine olan uzunluğun, alın bitiminden saç bitimine uzunluğa oranı 1,618’e yani altın orana eşittir.

Daha derine indiğimizde iç organlarımızda da altın oran vardır. Örneğin akciğerlerimizde soluk borumuzun devamında önce uzun ardından kısa bronşlar bulunur. Uzun bronşların uzunluğunu kısa bronşların uzunluğuna oranı da altın orandır.

Vücudumuzda yaşanan tüm olayları kontrol eden DNA’da altın oranın dikkat çekici örneklerinden biridir. DNA yapısal olarak iki sarmaldan oluşur ve bu sarmalların uzunluğu ve genişliği altın orana uygundur.

Hayvan bilimi olan zooloji de altın oran araştırma konusu olmuştur. Örneğin karıncanın gövdesinde yer alan her bir boğum ölçülüp oranlarına bakıldığında küçük parçanın büyüğe oranı ile büyük parçanın tüm karınca gövdesine oranı eşit olduğu görülür. Aynı incelemeler penguenler, sinekler, kelebekler, kaplanlar ve birçok hayvan üzerinde yapıldığında da altın orana rastlanmıştır.

Milattan önce yapılan yapılarda bile altın orana rastlanmaktadır. Örneğin nasıl yapıldığı hala gizemini koruyan, milattan önce 3000’li yıllarda yapıldığı düşünülen Mısır Piramitleri altın orana sahiptir. Piramitlerin yüksekliklerinin tabanları ile oranı, altın orana eşittir.

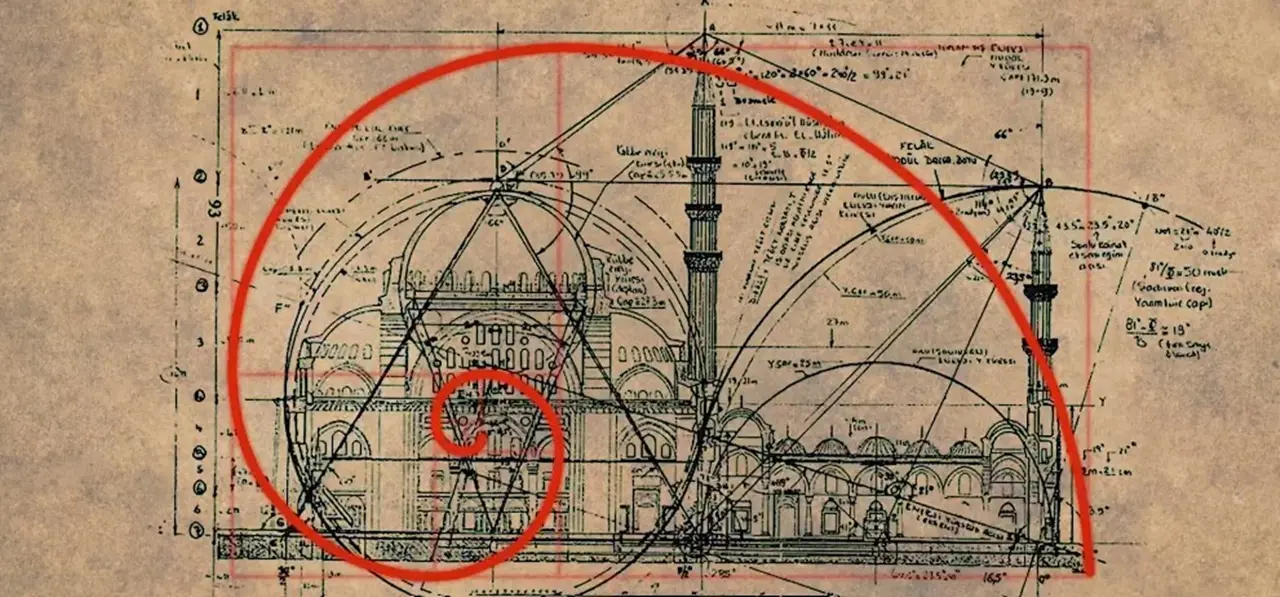
Türk mimarisinin öncüsü Mimar Sinan’ın eserleri bütünle ve kendileriyle bir oran içerisindedir. 1575 yılında tamamlanan Selimiye Cami ve 1557 yılından tamamlanan Süleymaniye Camiinde altın oran kullanılmıştır.  Sanat tarihinin önemli isimlerinden Celâl Esat Arseven’e göre özellikte Mimar Sinan’ın ustalık eseri Edirne Selimiye Caminin muazzam büyük ve geniş cephelerinde yer alan öğelerin yerleşiminde; kemer, kapı ve özellikle pencerelerin genişlik ve yükseklik ölçülerinde Sinan’ın altın oranın bilincinde olduğu görülmektedir.

Profesör mimar ve mimarlık tarihçisi Orhan Tuncer tarafından yapılan orantı analizleri sonucu Selçukluların 1258 yılında Konya’da inşa ettikleri İnce Minareli Medresesinin (1258) taç kapısı üzerinde kenar uzunlukları altın oranı veren dik üçgeninin varlığı ortaya çıkmıştır.

Mona Lisa tablosu, Mondrian Kırmızı, Sarı ve Mavi yağlı boya çalışması gibi ünlü eserler de altın oran göz önünde bulunarak resmedilmiştir.